日本の算額問題は凄い！

　講習Text表紙に何が良いかを考えて検索していたら、
明和水産の画像に出会いました。似たImageに
Wolfram Mathworldがあるのを思い出し、探したら、
この図を見つけました。10年以上前に解いた問題と
同じだったので、今回投稿します。

算額問題ですが、関連する事柄は多様で、学習に有益です。

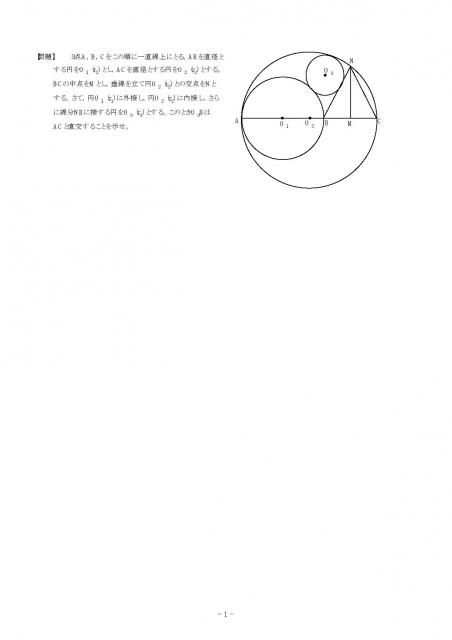
返信する

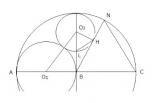
（つづき）
図を貼り忘れました。

まず強引に∠ＮＢＣを60°に取ります。
ＮＢ=ＢＣなので△ＮＢＣは正三角形であり、設問の二等辺三角形との条件も満たしています。（ここからが複雑）
Ｏ3から線ＮＢに垂線を引き、交点をHとする。
∠HＢＯ3は30°なので∠ＢＯ3Hは60°であり、△Ｏ3HＢは直角三角形。
その斜辺Ｏ3Ｂは上記値にして2であり、小円との交差地点（点Ｌとする）により二等分される。
直角三角形の斜辺を二等分しているので、Ｏ3Ｌ=ＬH。
Ｏ3Ｌ=ＬＢなのでＬH=ＬＢとなり、△ＬＢHは二等辺三角形三角形。
よって∠ＬＢH=∠ＬHＢ=30°であり、∠ＬHＯ3=60°。
△ＬHＯ3は二等辺三角形なので∠ＬＯ3H=60°であると同時に正三角形。
ということはＯ3Ｌ=Ｏ3HであるからＯ3Hは小円の半径。
Ｏ3HはＮＢへの垂線なので、小円は線ＮＢにずれずにぴったりと接していることになる。

以上ですが、これは図の様に中円の直径が大円の半径と等しいとき、設問の条件を満たす小円の中心Ｏ3は点Ｂで交差しているＡＣとの垂線上にある、ということです。
つまり中円が任意の大きさに変化する状況下では、あくまで「そういう瞬間ないし構図がある」ということを証明したに過ぎません。
でも自分としてはこれが精一杯です。
楽しみました、ありがとう。

返信する

この問題解けたら、何に応用できるの？

返信する

>>14
最後の行。「右辺」→「左辺」。
そろそろ訂正しておくね。

返信する