図形問題に挑戦しよう

▼ページ最下部

001 2011/01/26(水) 02:23:51 ID:4Oz.ZMk1Oo

Ｘの値を求める問題
三角関数を含まない答えを見つけて下さい。

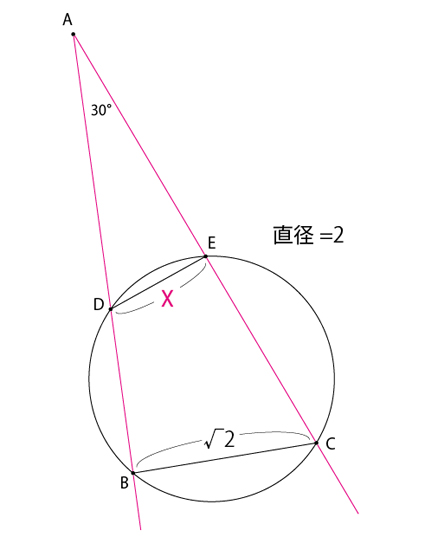
返信する

002 2011/01/27(木) 21:36:12 ID:j1Gr3mYPog

（√６−√２）／２

返信する

003 2011/01/30(日) 21:26:43 ID:/qA4WpUdvk

>>1
お〜い出題した人
∠ＢＥＣ＝１３５度のギロン→ムジュンはいらないのかい
フタバに見に行ったけどそのことふれずじまいでつ。

返信する

004 2011/01/30(日) 21:30:57 ID:ZuuL97de4w

>>3
∠ＢＥＣ＝４５度でしょう？

返信する

005 2011/01/30(日) 23:11:42 ID:UqpBE81Z/M

???俺全然わからんのやけど、これはAの位置がどこにあっても答えが同じになるらしいから、
∠ＢＥＣの角度って、固定されないんではないの？

ただ、Xの値は固定されるようだけど。∠ＢＥＣの角度は不定ではないの？
一定値なのかなぁ？？？　（××）わからへん。この分からず屋！　それって俺！

なんにしても俺にはわからない。ルートとか出てきた時点で。降参なんだけど。

返信する

006 2011/01/31(月) 21:34:16 ID:umdskxSTu.

∠ＢＥＣは弧ＢＣに対する円周角だからＥがどこでも一定だよ。

直径２から半径１
円の中心をＯとすると
ＯＢ：ＯＣ：ＢＣ＝１：１：√２だから
△ＯＢＣは直角二等辺三角形
∠ＢＯＣ＝９０°なので円周角は半分の４５°になる。

返信する

007 2011/02/01(火) 14:14:22 ID:W5QlSsBW6c

正直すまんかった。
勉強しなおさないとあかんね俺。
で、正解に至るまでの道、そろそろ教えてちょ〜。

返信する

008 2011/02/01(火) 19:46:01 ID:PD61zqTayU

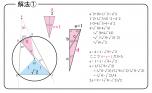
「中心角の半分が円周角」を基本に解いて下さい。

解法①

返信する

009 2011/02/01(火) 19:47:52 ID:PD61zqTayU

解法②

返信する

010 2011/02/01(火) 19:48:36 ID:PD61zqTayU

解法③

返信する

011 2011/02/01(火) 20:45:02 ID:dEZv5qpFgM

削除（by投稿者）

返信する

012 2011/02/01(火) 20:52:42 ID:dEZv5qpFgM

削除（by投稿者）

返信する

013 2011/02/01(火) 20:57:15 ID:dEZv5qpFgM

削除（by投稿者）

返信する

014 2011/02/02(水) 18:52:25 ID:cOkJDyiOPo

削除（by投稿者）

返信する

015 2011/02/02(水) 19:39:22 ID:cOkJDyiOPo

（細かいミスによる連続削除跡失礼m(__)m）

別解です。

２重根号がでてくるのが今ひとつです。

返信する

016 2011/02/13(日) 12:40:51 ID:a.ljKViNJA

面積Ｓの値は？

返信する

017 2011/02/13(日) 13:21:48 ID:yAM2FFzMvE

πr^2×140/360＝7πr^2/18

返信する

018 2011/02/14(月) 18:12:38 ID:trsILFg40g

・・・

返信する

019 2011/02/14(月) 20:42:43 ID:dAOBU01Y96

何で赤＋青が中心角２０度の扇形って言えるの？

返信する

020 2011/02/14(月) 21:13:12 ID:trsILFg40g

これでわかる？

返信する

021 2011/02/14(月) 23:43:16 ID:bzwGWIlRlo

>>18
二つの円のうち下の円の図で一番左端に青いのが残ってるのは間違いですわね？
つまんないこと言ってさーせん。面白い問題だね。

返信する

022 2011/02/15(火) 18:13:29 ID:YpckSlRQq6

>>21
ですね。左の青は消し忘れです。指摘ありがとう(^^;

変な形の図形の面積・立体の体積は
　「基本となる図形・立体の和や差で考える」
のがコツですね。

返信する

023 2011/02/15(火) 20:09:45 ID:Pv.IOEmpcM

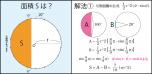>>16
いろいろ解答寄せて下さってありがとうございます。
解き方もいろいろあるので、参考になさって下さい。
解法２は、前出の寄せて下さった解答とダブるかも知れませんが悪しからず。
解法３については、>>17さんがその方法で解かれたように感じます。（以前も似た様な問題を出したことがあったので・・間違っていたらゴメンナサイ）

返信する

024 2011/02/15(火) 20:11:34 ID:Pv.IOEmpcM