探偵ナイトスクープで出た問題

とりあえず板にあったが流れるのでここに貼っておきます。
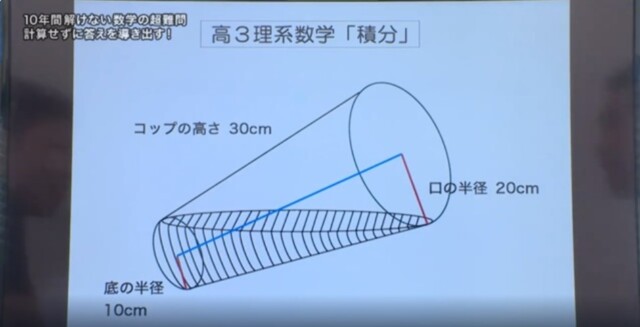
これを積分で解こうと思います。　計算式がかなり複雑になりそうな予感。
毎日少しづつ計算しようかとおもう。

返信する

s1=r(x)cosΘ・r(x)sinΘ
　=r(x)^2・sinΘcosΘ
　=r(x)^2・（1/2）sin2Θ

返信する

>>5
完全無欠のロックンローラー

返信する

Sx=r(x)＾2（kπ-(1/2)sin2Θ）　k=Θ/180

返信する

もしも、底の半径と口の半径が同じ２０だったらどうなるの？
そして、底の半径が０だった場合？

返信する

これはかなり難しい。　図形を用いてもそう簡単には解けない模様。

返信する

一応解答。　これも途中で吉田の公式よりと　訳の分からん公式が入る。　それ自体みんなが知ってるものでもないだろう。多分。

返信する

九九のメガネをかけた数学芸人がわかりやすく説明した

返信する

>>7
それはアラジン

スルーできんかったOrz

返信する

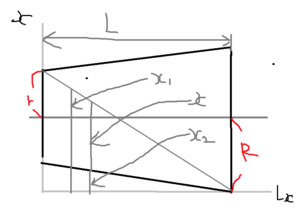
>>1図の　断面図

この斜めのラインの式を出して、　水が溜まっている所の高さｘを式として出します。

返信する

上の図より

x=-(2r/L)Lx＋2r

これと円の面積の式を結び付けて、積分で体積を求める公式が出せます。

返信する

ダメだわ。　断面積を求める公式までは出せるけど、その式が複雑すぎてとても積分なんかできる状態じゃない。
手詰まりです。　終わり。

返信する