垂線のひき方で…

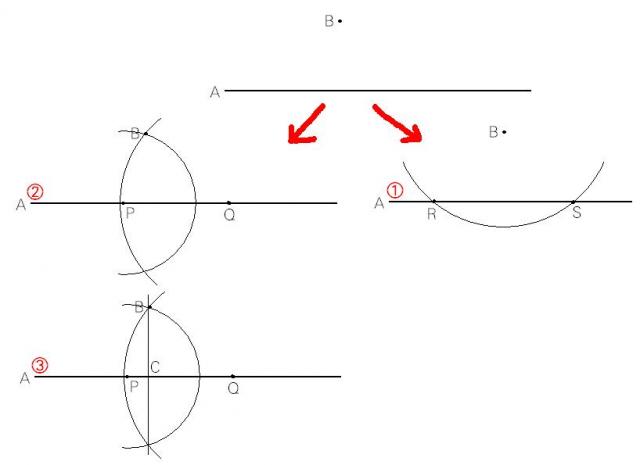
直線Ａ上ではない点Ｂから直線Ａへ垂線をひけ、という問題です。

一般的には①のように、点Ｂをコンパスの軸として直線Ａに２交点をとってから…ですが、
そうではない方法で、②の様に、任意の点ＰとＱを直線Ａ上にとり、
点Ｂを通るように点Ｐと点Ｑを中心とした半円をそれぞれ描きます。
点Ｂと対象の位置にある交点を求め、その点とＢを結んで③の様にしたとき、
直線Ａ⊥ＢＣとなります。

この場合、何で直線Ａ⊥ＢＣになるか、中学生の学習範囲で証明できますか。

返信する

教師だな貴様ｯ

返信する

よく知らないけど、証明っていうか「円の接線と半径」に関する定理なんじゃないの？

もし自分ならこんな感じで解答してみる

哿BPQは哿DPQと合い対する三辺の長さが等しいので対称形。
且つ、両図形における辺PQは同一かつ線A上にあるので、線Aに対して両図形は線対称形。
従って、頂点BとDも共に線Aに対して線対称の関係。
線対称にある点どうしを直線で結んだ場合、その線は対称線に対して直角に交わる。
よって、線Ａ⊥線ＢＣ。

返信する