垂線のひき方で…

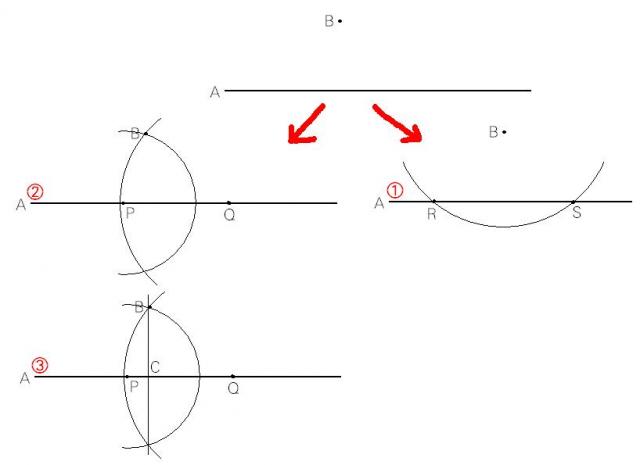
直線Ａ上ではない点Ｂから直線Ａへ垂線をひけ、という問題です。

一般的には①のように、点Ｂをコンパスの軸として直線Ａに２交点をとってから…ですが、
そうではない方法で、②の様に、任意の点ＰとＱを直線Ａ上にとり、
点Ｂを通るように点Ｐと点Ｑを中心とした半円をそれぞれ描きます。
点Ｂと対象の位置にある交点を求め、その点とＢを結んで③の様にしたとき、
直線Ａ⊥ＢＣとなります。

この場合、何で直線Ａ⊥ＢＣになるか、中学生の学習範囲で証明できますか。

返信する

教師だな貴様ｯ

返信する

よく知らないけど、証明っていうか「円の接線と半径」に関する定理なんじゃないの？

もし自分ならこんな感じで解答してみる

哿BPQは哿DPQと合い対する三辺の長さが等しいので対称形。
且つ、両図形における辺PQは同一かつ線A上にあるので、線Aに対して両図形は線対称形。
従って、頂点BとDも共に線Aに対して線対称の関係。
線対称にある点どうしを直線で結んだ場合、その線は対称線に対して直角に交わる。
よって、線Ａ⊥線ＢＣ。

返信する

>>3
の図をつかって適当に回答してみる。本当に適当なやつね。

三角形ＱＢＤも、三角形ＰＤＢも、二等辺三角形である。
両三角形は底辺を共有し、（高さが違う。）ているので、

両三角形の頂点を結ぶ線は、それぞれの二等辺三角形の底辺ＢＤを二分する点Ｃを通過する。
よってＢＤとＣＱは直角に交わる。

返信する

下の交点をＤとすると、

△ＢＰＱと△ＤＰＱにおいて
　仮定より（コンパスで作図したことから）
　　　ＢＰ＝ＤＰ
　　　ＢＱ＝ＤＱ
　またＰＱは共通
３辺がそれぞれ等しいので
△ＢＰＱ≡△ＤＰＱ

２つの三角形は直線Ａを対称の軸とする線対称な図形なので
対称の軸Ａは、対応する２点を結ぶ線分ＢＰを垂直に２等分する

よって、ＢＣ（ＢＤ）はＡＣに垂直である

返信する

２つの三角形は直線Ａを対称の軸とする線対称な図形なので
対称の軸Ａは、対応する２点を結ぶ線分ＢＰを垂直に２等分する


の２行目は、「線分ＢＤを垂直に２等分する」の間違い・・・orz

返信する

>>3
ＢＰ＝ＤＰ
ＢＱ＝ＤＱ
ＰＱ＝ＰＱ
３辺がそれぞれ等しいので
△ＢＰＱ≡△ＤＰＱ
∴∠BQP＝∠DQP

また
△BQCと△DQCにおいて
ＢＱ＝ＤＱ
ＰＱ＝ＰＱ
∠BQP＝∠DQP
∴△BQC≡△DQC
∴∠BCQ＝∠DCQ＝90°


以上より
直線Ａ⊥ＢＣ

返信する

なるほどですね。ところで無学な俺だけど

①後半はこう書き直した方がよさげ？（つまらん話だけど、つまりＰをＣに置き換え）
また
△BQCと△DQCにおいて
ＢＱ＝ＤＱ
ＱＣ＝ＱＣ
∠BQＣ＝∠DQＣ
∴△BQC≡△DQC
∴∠BCQ＝∠DCQ＝90°
以上より
直線Ａ⊥ＢＣ

②裏返しの図形でも
∴△BQC≡△DQC
と表記していいの？　いいのか。

③もし一行説明を足すとしたら
∴△BQC≡△DQC
線対称の図形である△BQC、△DQC は一辺ＱＣを共有し、辺ＢＣ、ＤＣが直線である。
∴∠BCQ＝∠DCQ＝90°
でいいですか？　あなたならどう書きますか？

返信する

削除（by投稿者）

返信する

>>8
点Cと点Pを書き間違えました
指摘どうもです

追加の一行は必要ないと思います

あえて書くとしたら

∴△BQC≡△DQC
∴∠BCQ＝∠DCQ
∠BCD＝180°より
∴∠BCQ＝∠DCQ＝90°
以上より
直線Ａ⊥ＢＣ

返信する

考えてみると当り前というか馬鹿々しくも難しい。

ここに底辺を同じくするa,b二つの二等辺三角形がある。
このとき互いの頂点どうしを結んだ線PQが、
それぞれにとって底辺と直角に交わる二等分線であることを証明せよ。
尚、線PQが底辺BDと交わる仮想点をCとする。

“正三角形の内角が全て等しいことを証明せよ”みたいな。

返信する

質問は「PQはBDを垂直に２等分することを証明せよ」って言い方がよく使われます。

（証明）
△BPQと△DPQにおいて
仮定よりPB=PD，QB=QD
PQは共通(で等しい)
３辺がそれぞれ等しいので
△BPQ≡△DPQ
よって∠BPQ(BPC)=∠DPQ(DPC)
二等辺三角形PBDの頂角BPDを２等分しているので
「二等辺三角形の頂角の二等分線の定理」より
PQ(PC)は底辺BDを垂直に２等分する
（以上）

（参考に）
定理名「二等辺三角形の頂角の二等分線の定理」は
本文が「二等辺三角形の頂角の二等分線は底辺を垂直に２等分する」です。
ってタイトルが本文の主語と全く同じ・・・



（「△ABCにおいて、AB=BC=CA ならば ∠A=∠B=∠Cである」ことの証明）

仮定よりAB=BC
二等辺三角形の２つの底角は等しいので
∠A=∠C
またBC=CAより同様にして∠B=∠A
よって、∠A=∠B=∠C

返信する

>>12
素晴しいっ！
>1の問題は突き詰めればこんな笑える問題になるね、ってつもりだったんだが
定理を使ってきちんと証明できるんだね。しかも冗談で書いた正三角形まで…。
数学って何事にも大真面目で面白い。

返信する

削除（by投稿者）

返信する

削除（by投稿者）

返信する

t

返信する