図形問題に挑戦しよう

Ｘの値を求める問題
三角関数を含まない答えを見つけて下さい。

返信する

∠ＢＥＣは弧ＢＣに対する円周角だからＥがどこでも一定だよ。

直径２から半径１
円の中心をＯとすると
ＯＢ：ＯＣ：ＢＣ＝１：１：√２だから
△ＯＢＣは直角二等辺三角形
∠ＢＯＣ＝９０°なので円周角は半分の４５°になる。

返信する

正直すまんかった。
勉強しなおさないとあかんね俺。
で、正解に至るまでの道、そろそろ教えてちょ〜。

返信する

「中心角の半分が円周角」を基本に解いて下さい。

解法①

返信する

解法②

返信する

解法③

返信する

削除（by投稿者）

返信する

削除（by投稿者）

返信する

削除（by投稿者）

返信する

削除（by投稿者）

返信する

（細かいミスによる連続削除跡失礼m(__)m）

別解です。

２重根号がでてくるのが今ひとつです。

返信する

面積Ｓの値は？

返信する

πr^2×140/360＝7πr^2/18

返信する

・・・

返信する

何で赤＋青が中心角２０度の扇形って言えるの？

返信する

これでわかる？

返信する

>>18
二つの円のうち下の円の図で一番左端に青いのが残ってるのは間違いですわね？
つまんないこと言ってさーせん。面白い問題だね。

返信する

>>21
ですね。左の青は消し忘れです。指摘ありがとう(^^;

変な形の図形の面積・立体の体積は
　「基本となる図形・立体の和や差で考える」
のがコツですね。

返信する

>>16
いろいろ解答寄せて下さってありがとうございます。
解き方もいろいろあるので、参考になさって下さい。
解法２は、前出の寄せて下さった解答とダブるかも知れませんが悪しからず。
解法３については、>>17さんがその方法で解かれたように感じます。（以前も似た様な問題を出したことがあったので・・間違っていたらゴメンナサイ）

返信する

解法２

返信する

解法3

返信する

三角関数はもう忘れました(^^;
（学校出てウン十年経つと……）

解法３は等式変形ですね、なるほど〜！

返信する

こちらに移動

返信する

教えてください。

この図の正三角形で以下の比例式が成立する根拠が分かりません。

h ： a ＝ X ： √３/２ * a

返信する

>>28
式中の大文字Ｘと図中の小文字ｘの関係がよく分からないけど
とりあえずhをbに置き換えると

b ： a ＝ X ： √３/２ * a

にはなると思うんだけど、何か参考になるでしょか。

返信する

>>29

誤ってエックスを大文字にしてしまいました。
すいません。

なぜ h を b に置き換えることができるのでしょうか。
数学は苦手なので、解りません。
教えてください。

返信する

>>30
いずれにせよ図中の小文字xが何を指すのか
更には斜線の部分の意味などが
私にはこの図の表記からはわかりません。
一番左のxの横に何か書いてある様にも見えるし。

＞なぜ h を b に置き換えることができるのか
線（x?）は大きい正三角形の頂点を通り底辺を等分しているので
その底辺とは直角に交わるっているのは確かだが、ついその調子で
hもその垂直２等分線と直角に交わっているもの（つまり底辺と平行）として
hを一辺とする小さい正三角形が出来ているものと決め付けてしまった。
よく考えてみるとそんな表記はないですね。実はhは斜めかも？
それとも直角に交わっている或いは底辺と平行である、と仮定すると
なぜhを一辺とする三角形が正三角形になるのかを尋ねているのでしょうか。
正三角形の３辺がそれぞれ等しい根拠を説明しろってことではないですよね。

返信する

説明不足でしたね。
すいません。

実は今、微分・積分の勉強をしているのですが、
さっぱり分からなくて、困っています。

xは大きな三角形を等分した線だと思います。
斜線部分（ΔS）は面積の増分（微小面積？）だそうです。

h ： a ＝ x ： √３/２ * a
h ＝ ２／√３ * x

という式がなぜ成立するのか分かりません。

返信する

>>32
もう来ないのかと思ったよ。
俺は微積分わからないから自分にわかる事だけ書いとく。

まず図>>28は三平方の定理から小文字の
x=√{a^2-(a/2)^2}
=√(a^2-a^2/4)
=√{(a^2)*3/4}
=a*√3/2（問題に記載がある）。

左図、線DEが辺BCと平行であるという前提で、
∠ABC=∠ADE=60°なので三角形ADEは正三角形。
よって線DE（=図28線h）＝線AE（=図29線b）

右図、左右の平行線を2:1で区切る同じく平行な中間線がある時、
線a,b,c,d,eは角度がどうであれ全て等しく2:1に区分される。

よって、線AE（=線h）：線AC（=線a）=図29X：図28x（=上記a*√3/2）
つまり、 h ： a＝X ： √３/２ * a
この等式は左片のaが右片では√３/２倍されているので
Xもhを√３/２倍したものでなければならない。
従って、X=h(√3/2)
h=X/(√3/2)
=X(2/√3)
=2/√3*X（>>32の式）

以上です。
ここは数学板なので微積分について正しく解説できる人もいると思います。
気長に待ってみては。

返信する

＞33さん

すいません。
平日はあまりパソコンをいじれないので。


詳しい解説ありがとうございます。
すごく分かりやすいです。
やっと疑問が解決しました。（＾＾）

これで先に進めます。

分からない問題に直面したら、またここに来ます。

それでは。

返信する

ああ良かった、と思いきや。
今にして思えば28図のaの位置にとらわれていたが為に、
聞かれた式に強引に合わせに行ってしまった様な…

考えてみれば大小の三角形は相似形なのに。
単純な話しをわざわざ複雑にしてしまった。
置き換える箇所間違えたな、反省。

返信する

とても丁寧で詳しい説明だったので、
分かりやすかったです。
感謝、感謝です。（＾＾）

返信する

こういう問題を時間内に一人で解くことがよく試験になるが、
むしろみんなで協力し合って解く能力のほうが重要じゃないか？

返信する

>>27
移動元の時から見てた。
今日までメモ帳にして80枚ぐらいやったけどわからなかった。
手計算では出ないのかも。

青い三角形の角度と面積が解れば出る。

返信する

>38
青い三角の面積は判った。√0.4375
その先はわからない

返信する

>>39
凄いね。
えっ？そこまで判る人が角度出ないの？
困った…
√2*X/2=√0.4375？・・・いややっぱ駄目だよ、角度わかんないと（汗

返信する

>>40
√2*X/2=√0.4375
X=√0.875
で？ Xを求めてどうしたいの？

返信する

>>41
あ〜〜そなの？ちょうど倍だね。
いやただ青い三角形の角度がわからないなら
せめて緑の三角形のA,bの角度出せるかなと思って。でも出せなかったし。
しかも出ても無理だわ・・・

>38の青三角形の鈍角をa,中角をb,鋭角をcとするなら
4π×c/360×2−2√0.4375＋π×（a−90）/360×2
でいいと思うんだよね。

返信する

削除（by投稿者）

返信する

削除（by投稿者）

返信する

>>43の間違いがわかりました。
Ｙが６個じゃなくて４個でした。あとマイナスの計算も。
4X+(π-2)*2-4=4Y
4X+2π-4-4=4Y
4X+6.28-8=4Y
4X-1.72=4Y
4X-4Y=1.72
X-Y=1.72/4
=0.43
で、連立も使えない。ただのお騒がせになってしまった。
スレ汚しなんで消しときます。悪夢だ…

返信する

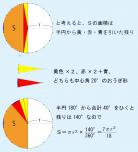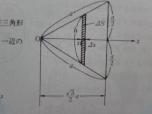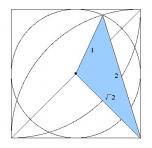
なんとか交点Pを特定しました。
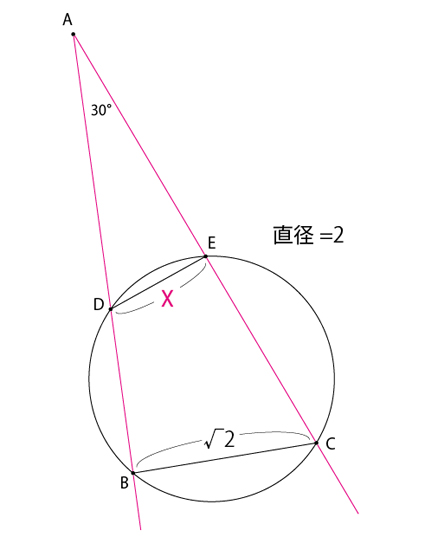
まず1rの扇形に関しては
x^2+y^2=1
且つ、2rの方は、
{(1-x)^2+(y+1)^2}=2^2
(1-x)(1-x)+(y+1)(y+1)=4
(1-1x-1x+x^2)+(y^2+1y+1y+1)=4
x^2-2x+1+y^2+2y+1=4
x^2-2x+y^2+2y=4-2
x^2+y^2-2x+2y=2
1rに関する式より、
(1)-2x+2y=2
-2x+2y=2-1
-x+y=0.5
y=x+0.5
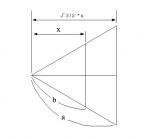
これを図に当てはめて考えると、
x^2+(x+0.5)^2=1
x^2+(x+0.5)(x+0.5)=1
x^2+(x^2+0.5x+0.5X+0.25)=1
2x^2+1x+0.25=1
2x^2+x=0.75
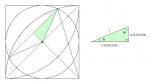
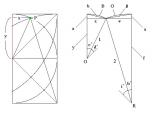
∴ x≒0.411, y≒0.911, a≒0.089, b≒0.421, e≒0.589, f≒1.911, g≒0.595
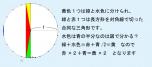
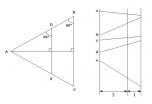
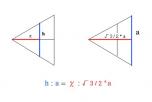
弧Bは弦bより長いはずなので少なくとも
c=24.126°以上となり、d=20.874°以下。
同様に弧Gも弦gより長いので少なくとも
h=17.060°以上であり、i=27.940°以下。
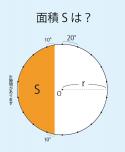
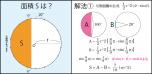
従って問題の面積は
両端の小扇形：1*1*π*d/360*2 に、
大扇形：2*2*π*i/360*2 から
三角形：f*1-y*x/2-f*e/2-1/2 を２つ引いた値を足すと、
0.364+1.950-0.661*2=0.991 になるので、大きくとも0.991以下。
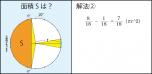
因みにこれまで知り得た最小値は
2*2*π/4-2*2/2-(2*2-1*1*π)/8*2=0.925 なので
大ざっぱだけど0.925以上0.991（単位２乗）以下、ってことで。

返信する

削除（by投稿者）

返信する

削除（by投稿者）

返信する

>>27
ｂ点の座標出た。
円の中心を原点とすると、x=(-1+√7)/4、y=(1+√7)/4
あとは知らん！

返信する

　　　　 ∧__∧
　　　　(　･ω･) 　　　ファルコンの定理
　　　　ﾊ∨/^ヽ
　　　ﾉ::[三ﾉ　:.'､
　　 i)､_;|*く;　　ﾉ
　　　　 |!: ::.".T‾
　　　　 ﾊ､___|
"""‾""""""‾"""‾"""‾"

返信する

おまいらそんなにこだわらずに文明の利器を使ってちゃっちゃと解いちゃえよ

都合上一辺2mになってるからな

返信する

>>51
手作業の尊さというものがあるんだよw
日本技術の基礎はそうやって培われて来た

返信する

「合ってるよ」って教えてくれたんだよ、きっと。

返信する

削除（by投稿者）

返信する