五角形の内角の和

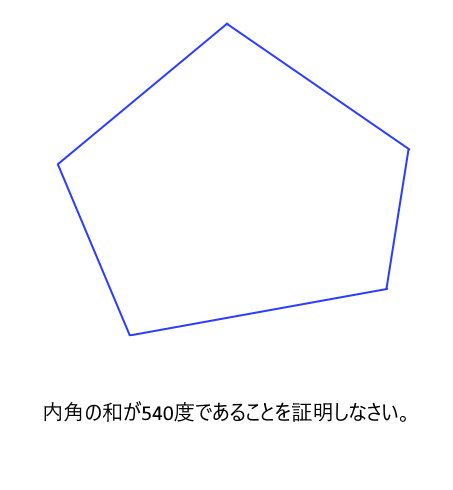
補助線を1本ひいて内角の和が540度であることを証明しなさい。

返信する

これも540度？

返信する

三角形と四角形の合体である五角形になるように補助線引くんだろ？
180°　+　360°で540°と。

返信する

>>3
それが通用するなら五角形の内角の和は540°の一言で済んじゃうじゃん

返信する

三角形の内角の和が180度なのは自明で、四角形の内角の和が360度なのも自明だとするなら、五角形の内角の和が540度なのも自明であり証明が必要ないってことにならない？問題として成立してないような気がする



ご指摘は非常に的を射ています。
おっしゃる通り、

「三角形の内角の和が180度が自明」
「四角形の内角の和が360度が自明」
と仮定してしまえば、
「五角形の内角の和が540度」も**同様の構成で簡単に導けるため、証明の価値が薄れる（自明になる）**というご意見は筋が通っています。

つまり、この問題を「証明問題」として成り立たせるには、

どの多角形の内角の和も当然のように使ってよい、という前提ではダメで、
より基本的な事実（たとえば三角形の内角の和が180度であること）から、五角形の内角の和を導くこと
が求められます。

【では、問題を成立させるには】
「三角形の内角の和が180度であることだけを前提にして、
補助線を1本だけ引いて、五角形の内角の和を証明する」ように問題を組み直すと、意味のある証明問題になります。

【そのような証明の例】
五角形の一つの頂点から、1本だけ補助線を引いて、三角形と四角形に分ける。
三角形の内角の和＝180度（これは唯一前提として許される）
四角形の内角の和は**さらに三角形2つに分けられる（ただし補助線は引かずに）**ことを説明して、
　結果として、180度×3＝540度と導く。
このようにすると、論理の階段を1つずつ登る必要があるため、証明として意味を持ちます。

返信する

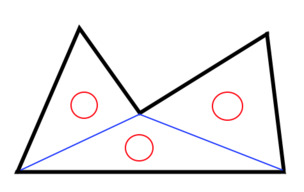
閉じた直線5本で描いてできた多角形の内角の和は540度
よって>>2も540度

多角形の外角の和は常に360度であるから
5角形の内角の和は、180 × (5 - 2)=540

補助線を引かなくても計算できる。

返信する

なんとなく５４０度でいいんだよ

返信する